SLAM系論文発表会を開催

2023年6月12日に弊社事務所にてSLAM系論文を読んで発表し合う会を開催しました。
https://deeplearning-oomiya.connpass.com/event/286506/

大政は「Simultaneous Localisation and Mapping (SLAM): Part 1 The Essential Algorithms」発表しました。

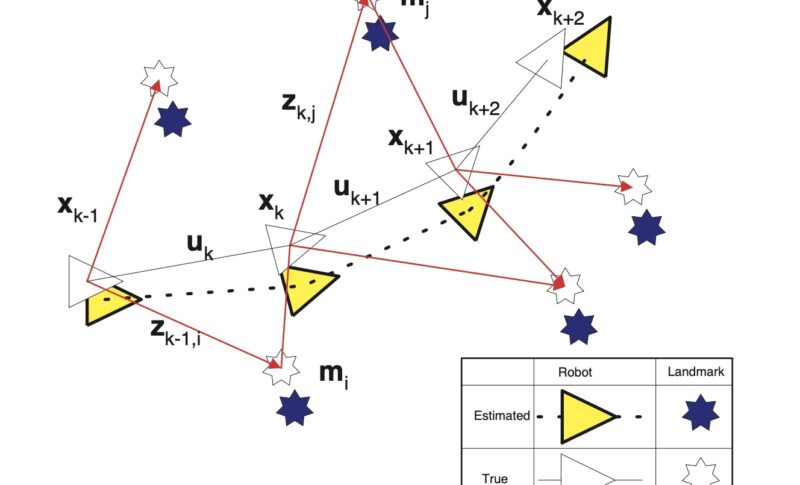
SLAMの目的は0時のロボットの位置\({\bf x}_0\)、control vectorの系列\({\bf u}_k\)、観測の系列\({\bf z}_k\)が与えら得た場合に、現在 k 時のロボットの位置\({\bf x}_k\)と全てのランドマークの３次元位置\({\bf m}\)を推定することである。つまりSLAMを定式化すると$$P \left( {\bf x}_{k}, {\bf m} \mid {\bf Z}_{0:k}, {\bf U}_{0:k}, {\bf x}_{0} \right)$$となる。これを解くため、まずモデルを observation modelとmotion modelに分け、さらに２種類のupdateを実施する。

1. observation model

k時にロボットからランドマークを観測した観測ベクトル\({\bf z}_{k}\)は k 時のロボット位置\({\bf x}_k\)とランドマークの３次元位置\({\bf m}\)から決まるはずなので、$$P \left( {\bf z}_{k} \mid {\bf x}_k, {\bf m} \right) $$とかける。

2. motion model

マルコフ性を仮定すると、k時のロボット位置\({\bf x}_k\)は k-1 時のロボット位置\({\bf x}_{k-1}\)と、そこから k 時位置までの遷移ベクトル（control vector：\({\bf u}_k\)で決まるはずなので、$$P \left( {\bf x}_{k} \mid {\bf x}_{k-1}, {\bf u}_k \right) $$とかける。

3. Time-update

\begin{eqnarray}
& P \left( {\bf x}_{k}, {\bf m} \mid {\bf Z}_{0:k-1}, {\bf U}_{0:k}, {\bf x}_{0} \right) \\
& = \int P \left( {\bf x}_{k} \mid {\bf x}_{k-1}, {\bf u}_k \right) \times P \left( {\bf x}_{k-1}, {\bf m} \mid {\bf Z}_{0:k-1}, {\bf U}_{0:k-1}, {\bf x}_{0} \right) {\rm d}{\bf x}_{k-1}
\end{eqnarray}

これをSLAM問題（１）式と比較すると、条件に k 時の観測ベクトル\({\bf z}_k\)が入ってない。つまりここまでは IMU・オドメトリなどの情報は用いるが、一方でランドマークの観測を用いずに推定している。

4. Measurement Update
time-updateで求めた x, m は観測ベクトル\({\bf z}_k\)が入ってないので、事前確率と考える。\({\bf z}_k\)を入れた事後確率を求めるとすると、ベイズの公式から

$$P \left( {\bf x}_{k}, {\bf m} \mid {\bf Z}_{0:k}, {\bf U}_{0:k}, {\bf x}_{0} \right) = \frac{P \left( {\bf z}_{k} \mid {\bf x}_k, {\bf m} \right) P \left( {\bf x}_{k}, {\bf m} \mid {\bf Z}_{0:k-1}, {\bf U}_{0:k}, {\bf x}_{0} \right)} {P \left( {\bf z}_{k} \mid {\bf Z}_{0:k-1}, {\bf U}_{0:k} \right)}$$

となる。右辺分子第１項目は観測モデルを尤度として用いている。

https://qiita.com/masataka46/items/a963addac6fff6ff94ac

この論文はSLAMにおける定式化の基礎に関するものであり、observation modelとmotion modelを定義し、time-updateとmeasurement-updateをベイズ的に繰り返すことによりlocalisationとmappingを同時に行うというものです。